深圳市初三上册数学期末试卷及答案

深圳市初三上册数学期末试卷及答案,标签：中考试题大全,http://www.kuaixue5.com
知，y=4时，x=80.5，矿工至少在爆炸后80.5﹣7=73.5（小时）才能下井．

　　解答：解：（1）因为爆炸前浓度呈直线型增加，所以可设y与x的函数关系式为y=k₁x+b（k₁≠0），

　　　　由图象知y=k₁x+b过点（0，4）与（7，46），

　　　　则，

　　　　解得，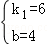

　　　　则y=6x+4，此时自变量x的取值范围是0≤x≤7．

　　　　（不取x=0不扣分，x=7可放在第二段函数中）

　　　　∵爆炸后浓度成反比例下降，

　　　　∴可设y与x的函数关系式为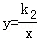（k₂≠0）．

　　　　由图象知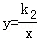过点（7，46），

　　　　∴，

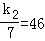　　　　∴k₂=322，

　　　　∴，此时自变量x的取值范围是x＞7． 

　　（2）当y=34时，由y=6x+4得，6x+4=34，x=5．

　　　　∴撤离的最长时间为7﹣5=2（小时）．

　　　　∴撤离的最小速度为3÷2=1.5（km/h）． 

　　（3）当y=4时，由y=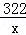得，x=80.5，

　　　　80.5﹣7=73.5（小时）．

　　　　∴矿工至少在爆炸后73.5小时才能下井．

点评：现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用待定系数法求出它们的关系式．

　　23．考点：相似三角形的判定与性质；等腰三角形的性质；勾股定理；正方形的性质．

　　专题：计算题．

　　分析：（1）作底边上的高，利用勾股定理求出高就可以求出面积．

（2）根据DE∥BC，得到△ADE∽△ABC，再根据相似三角形对应高的比等于相似比即可求出边DE的长度．

（3）根据△ADE∽△ABC得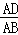=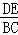，求出AD的长．

　　解答：解：（1）过A作AH⊥BC于H，

　　　　∵AB=AC=5，BC=6，

　　　　∴BH=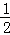BC=3，

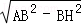　　　　∴AH===4，

　　　　∴S△ABC=BC•AH=×6×4=12． 

　　（2）令此时正方形的边长为a，

　　　　∵DE∥BC，

　　　　∴，

　　　　∴a=．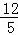

　　 （3）当AD=x时，由△ADE∽△ABC得=，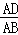

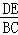　　　　即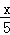

上一页  [1] [2] [3] [4] [5] [6] [7] [8]  下一页

上一篇：初三上册数学期末质量检测题及答案

你可能还感兴趣的《深圳市初三上册数学期末试卷及答案》相关文章

• 深圳市初三上册数学期末试卷及答案
• › 深圳市初三上册数学期末试卷及答案
• 在百度中搜索相关文章：深圳市初三上册数学期末试卷及答案
• 在谷歌中搜索相关文章：深圳市初三上册数学期末试卷及答案
• 在soso中搜索相关文章：深圳市初三上册数学期末试卷及答案
• 在搜狗中搜索相关文章：深圳市初三上册数学期末试卷及答案