(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34mg/L时,井下3km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
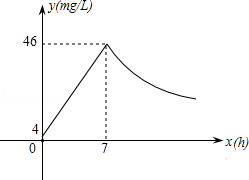
23.(9分)如图,在△ABC中,AB=AC=5,BC=6,D、E分别是边AB、AC上的两个动点(D不与A、B重合),且保持DE∥BC,以ED为边,在点A的异侧作正方形DEFG.
(1)试求△ABC的面积;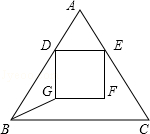
(2)当边FG与BC重合时,求正方形DEFG的边长;
(3)设AD=x,当△BDG是等腰三角形时,求出AD的长.
www.kuaixue5.com参考答案:
一、选择题(本部分共12小题,每小题3分,共36分.每小题给出4个选项,其中只有一个正确)
1.考点:简单组合体的三视图.
专题:几何图形问题.
分析:分别找到从正面,从上面看所得到的图形即可,注意所有的棱都应表现在主视图和俯视图中.
解答:解:如图所示,空心圆柱体的主视图是圆环;
俯视图是矩形,且有两条竖着的虚线.
故选B.
点评:本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
2.考点:一元二次方程的解;一元二次方程的定义.
分析:把x=1代入方程,即可得到一个关于m的方程,即可求解.
解答:解:根据题意得:(m﹣1)+1+1=0,
解得:m=﹣1.
故选B.
点评:本题主要考查了方程的解的定义,正确理解定义是关键.
3.考点:概率公式.
专题:压轴题.
分析:列举出所有情况,看上午选中台湾馆,下午选中法国馆的情况占总情况的多少即可.
解答:解:上午可选择3个馆,下午可选择3个馆,那么一共有3×3=9种可能,小明恰好上午选中台湾馆,下午选中法国馆这两个场馆的概率是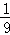 ,故选A.
,故选A.
点评:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=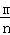 .
.
4.考点:三角形的角平分线、中线和高;三角形中位线定理.
专题:计算题.
分析:根据三角形的高、中线、角平分线的性质解答.
解答:解:因为在三角形中,
它的中线、角平分线一定在三角形的内部,
而钝角三角形的高在三角形的外部.
故选C.
点评:本题考查了三角形的高、中线和角平分线,要熟悉它们的性质方可解答.
5.考点:解一元二次方程-配方法.
分析:配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.
解答:解:∵x2﹣4x+3=0
∴x2﹣4x=﹣3
∴x2﹣4x+4=﹣3+4
∴(x﹣2)2=1
故选C.
点评:此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确应用.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
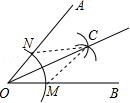
6.考点:全等三角形的判定与性质;作图—基本作图.
专题:证明题.
分析:连接NC,MC,根据SSS证△ONC≌△OMC,即可推出答案.
解答:解:连接NC,MC,
在△ONC和△OMC中
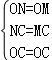 ,
,
∴△ONC≌△OMC(SSS),
∴∠AOC=∠BOC,
故选A.
点评:本题考查了全等三角形的性质和判定的应,主要考查学生运用性质进行推理的能力,题型较好,难度适中.
7.考点:由实际问题抽象出一元二次方程.
专题:增长率问题.
分析:第一次降价后的价格=原价×(1﹣降低的百分率),第二次降价后的价格=第一次降价后的价格×(1﹣降低的百分率),把相关数值代入即可.
解答:解:∵原价为200元,平均每次降价的百分率为x,
∴第一次降价后的价格=200×(1﹣x),
∴第二次降价后的价格=200×(1﹣x)×(1﹣x)=200×(1﹣x)2,
∴根据第二次降价后的价格为162元,列方程可得200(1﹣x)
上一页 [1] [2] [3] [4] [5] [6] [7] [8] 下一页
- 深圳市初三上册数学期末试卷及答案
- › 深圳市初三上册数学期末试卷及答案
- 在百度中搜索相关文章:深圳市初三上册数学期末试卷及答案
- 在谷歌中搜索相关文章:深圳市初三上册数学期末试卷及答案
- 在soso中搜索相关文章:深圳市初三上册数学期末试卷及答案
- 在搜狗中搜索相关文章:深圳市初三上册数学期末试卷及答案
