深圳市初三上册数学期末试卷及答案

深圳市初三上册数学期末试卷及答案,标签：中考试题大全,http://www.kuaixue5.com
　　故答案为：y=．

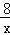点评：此题主要考查了用待定系数法求反比例函数的解析式，关键是正确把点的坐标代入函数解析式．

　　14．120

考点：翻折变换（折叠问题）；等边三角形的性质；正方形的性质．

　　分析：根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．

　　解答：解：∵正方形纸片ABCD分别沿AE、BF折叠，

　　∴AP=PB=AB，∠APB=60°．

　　∴∠EPF=120°．

　　故答案为：120．

点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称．

　　15．6037考点：规律型：图形的变化类．

　　分析：根据图形中点的个数得到有关棋子个数的通项公式，然后代入数值计算即可．

　　解答：解：观察图形知：

　　第1个图形有3+1=4个棋子，

　　第2个图形有3×2+1=7个棋子，

　　第3个图形有3×3+1=10个棋子，

　　第4个图形有3×4+1=13个棋子，

　　…

　　第n个图形有3n+1个棋子，

　　当n=2012时，3×2012+1=6037个，

　　故答案为：6037

点评：本题考查了图形的变化类问题，能够根据图形得到通项公式是解决本题的关键．

　　16．12考点：反比例函数系数k的几何意义．

　　专题：压轴题．

　　分析：先找到点的坐标，然后再利用矩形面积公式计算，确定k的值．

　　解答：解：由题意，设点D的坐标为（x_D，y_D），

　　则点B的坐标为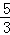（x_D，y_D），

　　矩形OABC的面积=|x_D×y_D|=，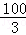

　　∵图象在第一象限，

　　∴k=x_D•y_D=12．

点评：本题考查了反比例函数与几何图形的结合，综合性较强，同学们应重点掌握．

　　三、解答题（本题共7小题，其中第17题5分，第18题6分，第19题8分，第20题7分，第21题8分，第22题9分，第23题9分，共52分）

　　17．

考点：解一元二次方程-配方法．

　　专题：压轴题．

　　分析：先移项，把2x移到等号的左边，再合并同类项，最后配方，方程的左右两边同时加上一次项系数一半的平方，左边就是完全平方式，右边就是常数，然后利用平方根的定义即可求解．

　　解答：解：∵x²﹣2x=2x+1，

　　∴x²﹣4x=1，

　　∴x²﹣4x+4=1+4，

　　　（x﹣2）²=5，

　　∴x﹣2=±，

　　∴x₁=2+，x₂=2﹣．

点评：此题考查了配方法解一元二次方程，配方法的一般步骤：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上一次项系数一半的平方；（4）选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．

　　18．考点：用样本估计总体；分式方程的应用．

　　专题：应用题．

　　分析：（1）等量关系为：4÷200=100÷鱼的总数，把相关数值代入计算即可；

（2）求得捞出鱼的总重量，除以捞出鱼的总条数即为一条鱼的重量，乘以鱼的总条数，再乘以每千克鱼的利润可得总利润．

　　解答：解：（1）设鱼塘中总共有x条鱼，由题意，

　　　　解得x=5000，经检验，x=5000是原方程的根．

　　　　答：鱼塘中总共有大约5000条鱼．

　　（2）解：塘中平均每条鱼约重（240+510）÷（100+200）=2.5（kg）；

　　　　塘中鱼的总质量约为2.5×5000=12500（kg）；

　　　　小江可获利润总额为12500×5=62500（元）

　　　　答：预计小江今年卖鱼总利润约62500元．

点评：考查用样本估计总体的有关计算；用样本概率估计总体是解决本题的思想；求得塘中平均每条鱼的重量是解决本题的易错点；用到的知识点为：样本容量越大，得到的数值越精确．

上一页  [1] [2] [3] [4] [5] [6] [7] [8]  下一页

上一篇：初三上册数学期末质量检测题及答案

你可能还感兴趣的《深圳市初三上册数学期末试卷及答案》相关文章

• 深圳市初三上册数学期末试卷及答案
• › 深圳市初三上册数学期末试卷及答案
• 在百度中搜索相关文章：深圳市初三上册数学期末试卷及答案
• 在谷歌中搜索相关文章：深圳市初三上册数学期末试卷及答案
• 在soso中搜索相关文章：深圳市初三上册数学期末试卷及答案
• 在搜狗中搜索相关文章：深圳市初三上册数学期末试卷及答案