深圳市初三上册数学期末试卷及答案

深圳市初三上册数学期末试卷及答案,标签：中考试题大全,http://www.kuaixue5.com

　　19．考点：全等三角形的判定与性质；平行四边形的性质．

　　专题：探究型．

　　分析：AF应该和CE相等，可通过证明三角形ADF和三角形BEC全等来实现．根据平行四边形的性质我们可得出：AD=BC，∠A=∠C，∠ADC=∠ABC，因为DF和BE是∠ADC，∠CBA的平分线，那么不难得出∠ADF=∠CBE，这样就有了两角夹一边，就能得出两三角形全等了．

　　解答：解：AF=CE．理由如下：

　　∵四边形ABCD是平行四边形，

　　∴AD=CB，∠A=∠C，∠ADC=∠ABC，

　　又∵∠ADF=∠ADC，∠CBE=∠ABC，

　　∴∠ADF=∠CBE，

　　在△ADF和△CBE中，

　　

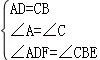
　　∴△ADF≌△CBE（AAS），

　　∴AF=CE．

点评：求某两条条线段相等，可通过证明他们所在的三角形全等来实现，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．

　　20．考点：相似三角形的应用．

　　专题：应用题．

　　分析：过点A作AH⊥EF于H点，AH交CD于G，根据EF∥AB∥CD可求出EF、HB、GD，再根据相似三角形的判定定理可得△ACG∽△AEH，再根据三角形的相似比解答即可．

　　解答：解：过点A作AH⊥EF于H点，AH交CD于G，

　　∵CD∥EF，

　　∴△ACG∽△AEH，

　　∴，

　　即：，

　　∴EH=12.4．

　　∴EF=EH+HF=12.4+1.6=14，

　　∴旗杆的高度为14米．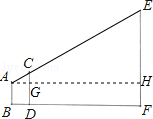

点评：此题难度不大，解答此题的关键是作出辅助线．构造出相似三角形，利用平行线的性质及相似三角形的相似比解答．

　　21．考点：一元二次方程的应用．

　　专题：增长率问题．

　　分析：（1）设每千克核桃降价x元，利用销售量×每件利润=2240元列出方程求解即可；

（2）为了让利于顾客因此应下降6元，求出此时的销售单价即可确定几折．

　　解答：（1）解：设每千克核桃应降价x元．   …1分        

　　根据题意，得  （60﹣x﹣40）（100+×20）=2240．  …4分        

　　化简，得  x²﹣10x+24=0    解得x₁=4，x₂=6．…6分

　　答：每千克核桃应降价4元或6元．   …7分 

（2）解：由（1）可知每千克核桃可降价4元或6元．        

　　因为要尽可能让利于顾客，所以每千克核桃应降价6元．           

　　此时，售价为：60﹣6=54（元），． …9分

　　答：该店应按原售价的九折出售．  …10分

点评：本题考查了一元二次方程的应用，解题的关键是根据题目中的等量关系列出方程．

　　22．考点：反比例函数的应用；一次函数的应用．

　　专题：应用题；压轴题．

　　分析：（1）根据图象可以得到函数关系式，y=k₁x+b（k₁≠0），再由图象所经过点的坐标（0，4），（7，46）求出k₁与b的值，然后得出函数式y=6x+4，从而求出自变量x的取值范围．再由图象知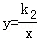（k₂≠0）过点（7，46），求出k₂的值，再由函数式求出自变量x的取值范围．

（2）结合以上关系式，当y=34时，由y=6x+4得x=5，从而求出撤离的最长时间，再由v=速度．

（3）由关系式y=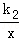

上一页  [1] [2] [3] [4] [5] [6] [7] [8]  下一页

上一篇：初三上册数学期末质量检测题及答案

你可能还感兴趣的《深圳市初三上册数学期末试卷及答案》相关文章

• 深圳市初三上册数学期末试卷及答案
• › 深圳市初三上册数学期末试卷及答案
• 在百度中搜索相关文章：深圳市初三上册数学期末试卷及答案
• 在谷歌中搜索相关文章：深圳市初三上册数学期末试卷及答案
• 在soso中搜索相关文章：深圳市初三上册数学期末试卷及答案
• 在搜狗中搜索相关文章：深圳市初三上册数学期末试卷及答案