∵BC∥AD， ∴∠BCE=∠DEC，∴∠AFE=∠DEC ①，
∵点A与点D关于
轴对称，而C，O在对称轴上，
∴△ACO与△DCO关于轴对称，
∴∠FAE=∠EDC ②， 由①，②得△AEF∽△DCE；…………………8分
（3）当FE=EC时，△EFC为等腰三角形，由（2），△AEF∽△DCE，∴FE:EC=AE:DC，此时，AE=DC=AC=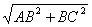
=20，则E（8，0）；
当CF=CE时，∠CFE=∠CEF=∠ACB，则有EF∥BC，
此时，点F与A重合，则点E在D处，与已知矛盾；
当CF=FE时，∠FCE=∠CEF，又∵△AEF∽△DCE，∴∠AEF=∠DCE
∴∠FCE+∠DCE =∠CEF+∠AEF，即∠ACD=∠AEC， 而∠CAE=∠DAC，
∴△AEC∽△ACD，AE:AC=AC:AD，而AD=18，∴AE=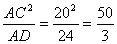
则E（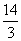
，0），
∴当△EFC为等腰三角形时，点E的坐标为（8，0）或（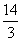
，0）…12分(每个E点坐标给2分)
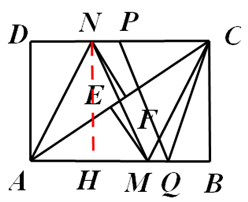
28.（1）证明：∵四边形ABCD是矩形，∴∠D=∠B，AD=BC，AD∥BC∴∠DAC=∠BCA
又由翻折的性质，得∠DAN=∠NAF，∠ECM=∠BCM，∴∠DAN=∠BCM
∴△AND≌△CBM（ASA） ………………………………………………3分
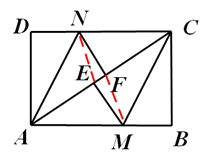
（2）证明：∵△AND≌△CBM，∴DN=BM
又由翻折的性质，得DN=FN，BM=EM， ∴FN=EM
又∠NFA=∠ACD＋∠CNF=∠BAC＋∠EMA=∠MEC，
∴FN∥EM。∴四边形MFNE是平行四边形 ………6分
四边形MFNE不是菱形，……………………………7分
理由如下：
由翻折的性质，得∠CEM=∠B=900，
∴在△EMF中，∠FEM＞∠EFM
∴FM＞EM。∴四边形MFNE不是菱形 …………………………8分
（3）解：∵AB=4，BC=3，∴AC=5
设DN=x，则由S△ADC=S△AND＋S△NAC得
×3 x＋×5 x=×12，解得x=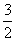
，即DN=BM=
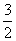……………9分
过点N作NH⊥AB于H，则HM=4－2×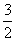=1
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] 下一页
- 2017年靖江九年级数学期中试卷及答案
- › 国土局2017年工作总结及2017年工作计划
- › 2017年乡镇党风廉政建设总结
- › 县开发局2017年工作思路
- › 镇2017年人口与计划生育工作总结
- › 2017年机械分公司党支部工作总结
- › 国税局2017年度工作总结
- › 2017年扶贫工作总结
- › 2017年度地震局工作总结
- › 地方税务局2017年工作总结
- › 县电教室2017年工作总结
- › 2017年导航站工作总结
- › 2017年组织部工作总结
- 在百度中搜索相关文章：2017年靖江九年级数学期中试卷及答案
- 在谷歌中搜索相关文章：2017年靖江九年级数学期中试卷及答案
- 在soso中搜索相关文章：2017年靖江九年级数学期中试卷及答案
- 在搜狗中搜索相关文章：2017年靖江九年级数学期中试卷及答案