扇形的的弧长=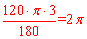
（cm），扇形的面积=
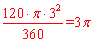（cm2）。
三、解答题
1. （2001江苏常州6分）已知：如图，△ABC内接于⊙O，AE切⊙O于点A，BD∥AE交AC的延长线于点D，求证：AB2=AC•AD
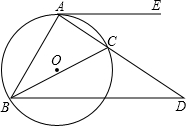
【答案】证明：∵BD∥AE，∴∠EAD=∠D。
∵AE切⊙O于点A，∴∠EAD=∠ABC。∴∠ABC=∠D。
∵∠BAC=∠DAB，∴△ACB∽△ABD。∴AB：AD=AC：AB。∴AB2=AC•AD。
【考点】弦切角定理，相似三角形的判定和性质。
【分析】欲证AB2=AC•AD，即证AB：AD=AC：AB，可以通过证明△ABC∽△ABD得出．而已知∠BAD公共，又可以根据已知条件推出∠ABC=∠D，由两角对应相等的两个三角形相似，得出△ACB∽△ABD，从而得到结论。
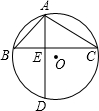
2. （2001江苏常州6分）已知：如图，⊙O的弦AD、BC互相垂直，垂足为E，∠BAD＝∠α，∠CAD＝∠β，且siaα=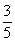
， cosβ=
，AC=2，求（1）EC的长；（2）AD的长。
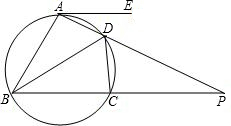
3. （江苏省常州市2002年6分）如图，四边形ABCD内接于⊙O，边AD，BC的延长线相交于点P，直线AE切⊙O于点A，且AB×CD=AD×PC，求证：（1）△ABD∽△CPD； （2）AE∥BP。
【答案】证明：（1）∵四边形ABCD内接于⊙O，∴∠BAD=∠DCP。
又∵AB•CD=AD•PC，∴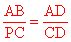
。∴△ABD∽△CPD。
（2）由（1）得∠ABD=∠P。
又∵AE为切线，AD为弦，∴∠EAD=∠ABP，即∠P=∠EAD。
∴AE∥BP。
【考点】圆内接四边形的性质，切线的性质，相似三角形的判定和性质，平行的判定。
【分析】（1）已知AB•CD=AD•PC，即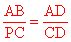，所以要证△ABD∽△CPD，只需证得两组对应边的夹角相等即可，而这组角可通过圆内接四边形的性质求得。
（2）在（1）的基础上，可求得∠ABD=∠P；根据弦切角定理可求得∠EAD=∠ABD，即∠EAD=∠P；内错角相等，可证得两直线平行。
4. （江苏省常州市2003年6分）如图，已知AB是⊙O的直径，C是⊙O上一点，连接AC，过点C作直线CD⊥AB于点D，E是AB上一点，直线CE与⊙O交于点F，连结AF，与直线CD交于点G。
求证：（1）∠ACD=∠F； （2）AC2=AG·AF。
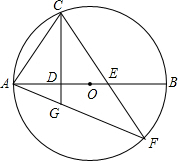
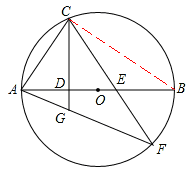
【答案】证明：（1）连接BC，则∠ACB=90°，∠ABC=∠F。
∵∠ACD+∠CAD=90°，∠CAD+∠ABC=90°，
∴∠ACD=∠ABC。∴∠ACD=∠F。
（2）由（1）得出的∠ACD=∠F，
又∵∠CAG=∠FAC，∴△ACG∽△AFC。
∴
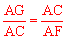。∴AC2=AG•AF。
【考点】圆周角定理，相似三角形的判定和性质
【分析】（1）本构建相等的中间角通过转换来求解，连接BC，根据圆周角定理得∠ABC=∠F，根据同角的余角相等得∠ACD=∠ABC，由此可得证。
（2）要证AC2=AG·AF，即要AC：AG=AF：AC即可，只要△ACG∽△AFC。已知了一个公共角，而（1）中又证得了∠ACD=∠F，由此可得出两三角形相似，根据相似三角形即可得出所求的比例关系。
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] 下一页
- 圆形练习题及答案（五）
- › 圆形练习题及答案（十）
- › 圆形练习题及答案（五）
- › 圆形练习题及答案（六）
- › 圆形练习题及答案（七）
- › 圆形练习题及答案（八）
- › 圆形练习题及答案汇总
- 在百度中搜索相关文章：圆形练习题及答案（五）
- 在谷歌中搜索相关文章：圆形练习题及答案（五）
- 在soso中搜索相关文章：圆形练习题及答案（五）
- 在搜狗中搜索相关文章：圆形练习题及答案（五）