【答案】B。
【考点】两圆的位置关系。
【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。因此：
∵两半径之差7－3等于两圆圆心距4，∴两圆内切。故选B。
www.kuaixue5.com二、填空题
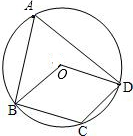
1. （2001江苏常州3分）已知：如图，四边形ABCD内接于⊙O，若∠BOD＝1200，OB＝1，则∠BAD= 度，∠BCD＝ 度，弧
的长＝ .
【答案】60；120；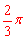
。
【考点】圆周角定理，圆心角、弧、弦的关系，圆内接四边形的性质，弧长的计算。
【分析】∵∠BOD和∠BOD是同弧所对的圆周角和圆心角，且∠BOD=120°，
∴∠BA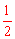D=
∠BOD=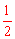×120°=60°。
∵四边形ABCD内接于⊙O，∴∠BCD=180°－∠BAD=180°－60°=120°。
∵∠BOD=120°，OB=1，∴弧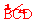
的长=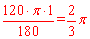
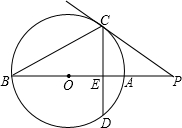
2. （2001江苏常州3分）已知：如图，PC切⊙O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，PC＝4，PB＝8，则PA＝ ▲ ，sin∠P= ▲ ，CD= ▲ .
【答案】2；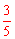
；
。
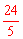【考点】切割线定理，垂径定理，切线的性质，锐角三角函数定义
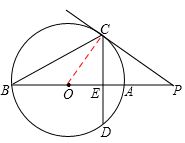【分析】∵PC切⊙O于点C，割线PAB经过圆心O，PC=4，PB=8，
∴PC2=PA•PB
【注：没学习切割线定理可连接AC，通过证明△ACP∽△CBP得到】
∵PC＝4，PB＝8，
∴PA=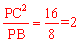
。
∴AB=6。∴圆的半径是3。
连接OC，∵OC=3，OP=5，∴sin∠P=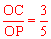
。
∵CD⊥AB于点E，∴CD=2CE。
∵CE=
。∴CD=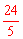
3. （江苏省常州市2002年2分）已知记扇形的圆心角为1500，它所对的弧长为20πcm，则扇形的半径为 cm，扇形的面积是 cm2.
【答案】24；
。
【考点】扇形面积的计算，弧长的计算。
【分析】根据弧长公式求出半径，根据面积公式求面积：
∵根据已知和弧长公式，得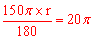
，∴r=24cm。
∴根据面积公式，得扇形的面积=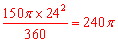
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] 下一页
- 圆形练习题及答案（五）
- › 圆形练习题及答案（十）
- › 圆形练习题及答案（五）
- › 圆形练习题及答案（六）
- › 圆形练习题及答案（七）
- › 圆形练习题及答案（八）
- › 圆形练习题及答案汇总
- 在百度中搜索相关文章：圆形练习题及答案（五）
- 在谷歌中搜索相关文章：圆形练习题及答案（五）
- 在soso中搜索相关文章：圆形练习题及答案（五）
- 在搜狗中搜索相关文章：圆形练习题及答案（五）