.
于是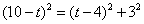 .解处
.解处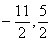 . ………………(9分)
. ………………(9分)
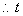 的值为
的值为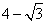 或4或
或4或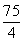 ……………………………(10分)
……………………………(10分)
28.解:(1)A(2,0),B(―8,―5).…………(1分)
∴抛物线的函数关系式为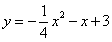 …………(3分)
…………(3分)
(2)当∠BPA=90º时,由PA=PB,构造两个全等的直角三角形,…………………(4分)
根据全等得出P点为(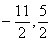 ), …………………(6分)
), …………………(6分)
代入抛物线方程,显然不成立,∴点P不存在………………(7分)
∴不存在点P,使△PAB恰好是一个等腰直角三角形.
 (3)设P(m,
(3)设P(m,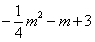 ),则D(m,
),则D(m,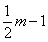 ).
).
∴PD=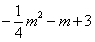 ―(
―(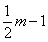 )
)
=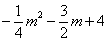
=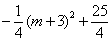 .………………(8分)
.………………(8分)
∴当m=―3时,PD有最大值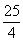 .
.
此时⊙E在直线AB上截得的线段的长度最大. ………(9分)
过E作EF⊥AB于点F,由△DEF∽△GAO可得:
DF= ,所以截得的最长线段为
,所以截得的最长线段为 .………(10分)
.………(10分)
上一页 [1] [2] [3] [4] [5] [6] [7]
- 江阴市初三上册数学期末试卷及答案
- › 江阴市初三上册数学期末试卷及答案
- 在百度中搜索相关文章:江阴市初三上册数学期末试卷及答案
- 在谷歌中搜索相关文章:江阴市初三上册数学期末试卷及答案
- 在soso中搜索相关文章:江阴市初三上册数学期末试卷及答案
- 在搜狗中搜索相关文章:江阴市初三上册数学期末试卷及答案
