| 平均数 | 众数 | 中位数 | 方差 | |
| 甲组 | 8 | 8 | 8 | 1.6 |
| 乙 | 8 |
（表一） （表二）
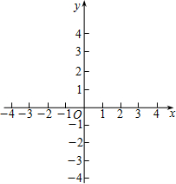
（1）根据表一中统计的数据，完成表二；
（2）请你从平均数和方差的角度分析，哪组的成绩更好些？
24．（本题满分8分）已知二次函数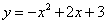
．
（1）求抛物线顶点M的坐标；
（2）设抛物线与x轴交于A，B两点，与y轴交于C点，求A，B，C的坐标（点A在点B的左侧），并画出函数图象的大致示意图；
（3）根据图象，求不等式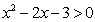
的解集
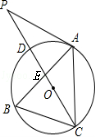25．（本题满分8分）如图，点A、B、C分别是⊙O上的点， CD是⊙O的直径，P是CD延长线上的一点，AP=AC．
（1）若∠B=60°，求证：AP是⊙O的切线；
（2）若点B是弧CD的中点，AB交CD于点E，CD=4，求BE·AB的值.
26．（本题满分8分）某果园有100棵橙子树，每一棵树平均结600个橙子．现准备多种一些橙子树以提高产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少．根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子．
（1）如果多种5棵橙子树，计算每棵橙子树的产量；
（2）如果果园橙子的总产量要达到60375个，考虑到既要成本低，又要保证树与树间的距离不能过密，那么应该多种多少棵橙子树？
（3）增种多少棵橙子树，可以使果园橙子的总产量最多？最多为多少？
27．（本题满分10分） 
如图，矩形ABCD，A（0，3）、B（6，0），点E在OB上，∠AEO=30°，点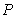
从点Q（-4，0）出发，沿x轴向右以每秒1个单位长的速度运动，运动时间为t秒．
（1）求点E的坐标；
（2）当∠PAE=15°时，求t的值；
（3）以点P为圆心，PA为半径的
随点P的运动而变化，当与四边形AEBC的边（或边所在的直线）相切时，求t的值．
28．（本题满分10分）如图，在平面直角坐标系中，直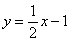线
与抛物线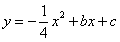
交于A、B两点，点A在x轴上，点B的横坐标为－8．点P是直线AB上方的抛物线上的一动点（不与点A、B重合）．
（1）求该抛物线的函数关系式；
（2）连接PA、PB，在点P运动过程中，是否存在某一位置，使△PAB恰好是一个以点P为直角顶点的等腰直角三角形，若存在，求出点P的坐标；若不存在，请说明理由；
（3）过P作PD∥y轴交直线AB于点D，以PD为直径作⊙E，求⊙E在直线AB上截得的线段的最大长度．
上一页 [1] [2] [3] [4] [5] [6] [7] 下一页
- 江阴市初三上册数学期末试卷及答案
- › 江阴市初三上册数学期末试卷及答案
- 在百度中搜索相关文章：江阴市初三上册数学期末试卷及答案
- 在谷歌中搜索相关文章：江阴市初三上册数学期末试卷及答案
- 在soso中搜索相关文章：江阴市初三上册数学期末试卷及答案
- 在搜狗中搜索相关文章：江阴市初三上册数学期末试卷及答案