由图可知： 12a=5a+5b+12b， 整理得： 7a=17b
12b+4b+4c=12c， 整理得： 2b=c
甲步行： 4 （ b+c ） ， 乙步行： 5 （ a+b ），
甲乙步行路程比为： 4 （ b+c ） :5(a+b)=4(b+2b):5(17b/7 +b)=12b:120b/7=7:10
二、解答题（每小题15分，共60分）
每题都要写出推算过程。
13.一辆汽车从甲地开往乙地，若车速提高 20% ，可提前 25 分钟到达；若以原速行驶 100 千米，再将车速提高 25% ，可提前 10 分钟到达。求甲乙两地的距离。
解析： 原 车速为 1 ，若提速 20% ，则提前 25 分钟，在相同的时间下，提速后比原速多行了 25*1
提速后行完全程所用时间为： 25*1/20%= 125 分钟，原速所用时间为 125+25 分 =150 分钟
若以原速行驶 100 千米后，再提速 25% ，提前 10 分钟，全程用时 140 分钟。则 100 千米后的路程所用时间为： 10*1/25%=40 分，说明 100 千米用时 100 分钟，原速度为 1 千米 / 分钟，
所以甲乙两地之间距离为 150 千米。
( 注意：我又列方程验证了，虽然很麻烦，但是我也希望你能用不同的方法来验证 )
www.kuaixue5.com
14.如图，在一个棱长为 20 厘米的正方体密闭容器的下底固定一个实心圆柱体，容器内盛有 
升水时，水面恰好经过圆柱体的上底面。如果将容器倒置，圆柱体有 8 厘米露出水面。已知圆柱体的底面积是正方体底面积的 
，求实心圆柱体的体积。
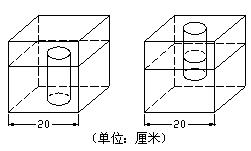
解析：水的体积没有变。设圆柱体的高度为 x 厘米。 水的体积做等量关系。
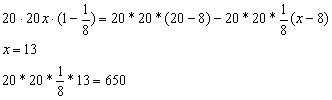
15.有 8 个足球队进行循环赛，胜队得 1 分，负队得 0 分，平局的两队各得 0.5 分。比赛结束后，将各队得分按从高到低排名后发现：各队得分互不相同，且第 二名的得分与最后四名所得总分一样多。求这次比赛中，第二名的队的 得分。
解析： 这道题是一道逻辑推理题：
刚开始的思路是：最后一名得 0 分，依次为 0 、 0.5 、 1 、 1.5则第二名得 3 分。
8 个足球队进行循环赛，要踢 8*7/2=28 场比赛。也就是说， 8 个队的得分总和应为 28 分。
若第二名得 3 分，则第一名得分大于 8 分。此思路不行。
再思考：刚才绕远了。设若第一支足球队赢了其他 7 个队，得最高分 7 分，其它队依次为： 6 、 5 、 4 、 3 、 2 、 1 、 0. 这样第二名 6 分，正好等于最后四名的总分 6. 因此第二名得分为 6 分，正好。
16.将两个不同的自然数中较大的数换成它们的差，称为一次操作，如此继续下去，直到这两个数相同为止。如对 20 和 26 进行这样的操作，过程如下：
（ 20 、 26 ） → （ 20 、 6 ） → （ 14 、 6 ） → （ 8 、 6 ） → （ 2 、 6 ） → （ 2 、 4 ） → （ 2 、 2 ）
（ 1 ）对 45 和 80 进行上述操作。
操作：（ 45，80 ） --- （ 45，35 ） --- （ 10，35 ） --- （ 10，25 ） --- （ 10，15 ） --- （ 10，5 ） --- （ 5，5 ）
（ 2 ）若对两个四位数进行上述操作，最后得到的相同数是 17 ，求这两个四位数的和的最大值。
操作：逆推 和最大： （ 17，17 ） --- （ 17，34 ） --- （ 51，34 ）
因为要求和的最大值，可发现和的规律：
17*2---17*3---17*5---17*8---17*13---17*21---17*34---17*55---17*89---17*144---17* 233
17 要乘以斐波那契数列，两个四位数的和不会超过 20000 ，即最大是 17*1176. 但是 1176 是不是斐波那契数列的最后一环还要试下去： 17*377---17*610---17*987---17*1597，1597 大于 1176 ，因此和最大是： 17*987=16779
总结：做题要判断这道题可能是什么类型，然后去按想到的思路走一走。尝试的过程不怕麻烦，不怕做不出来。若思路不对，再换思路。
所考的知识点要注意总结：
（1） 循环小数和分数的互化
（2） 找规律
（3） 连续自然数的和（ 1+2+3+……+10=55 等）
上一页 [1] [2] [3] [4] [5] [6] 下一页
- 第九届小学希望杯第2试真题解析（六年级）
- › 第九届小机灵杯五年级初赛试题
- › 第九届小机灵杯四年级初赛试题
- › 第九届小机灵杯三年级复赛试题
- › 第九届小学希望杯第2试真题解析（六年级）
- › 第九届小学希望杯五年级第2试试卷
- › 第九届小学希望杯四年级第2试
- › 第九届小学希望杯六年级第1试真题试卷
- › 第九届小学希望杯四年级第1试真题试卷
- › 第九届小学希望杯五年级第1试真题试卷
- 在百度中搜索相关文章：第九届小学希望杯第2试真题解析（六年级）
- 在谷歌中搜索相关文章：第九届小学希望杯第2试真题解析（六年级）
- 在soso中搜索相关文章：第九届小学希望杯第2试真题解析（六年级）
- 在搜狗中搜索相关文章：第九届小学希望杯第2试真题解析（六年级）