2017高考数学复习：数列（二）

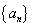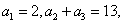2．在等差数列中，已知则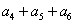＝     42    。

3．已知等差数列共有10项，其中奇数项之和15，偶数项之和为30，则其公差是    3    。

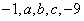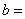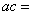4．如果成等比数列，则    3     ，      -9      。

5．设等差数列{an}的前n项和为Sn，已知a3=12，S12>0，S13<0.

(1)求公差d的取值范围；

(2)指出S1、S2、…、S12中哪一个值最大，并说明理由.

解：(1)依题意有：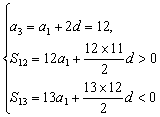

解之得公差d的取值范围为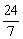－＜d＜－3.

(2)解法一：由d＜0可知a1>a2>a3>…>a12>a13，因此，在S1，S2，…，S12中Sk为最大值的条件为：ak≥0且ak+1＜0，即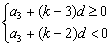

∵a3=12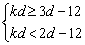，  ∴， ∵d＜0，  ∴2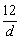－＜k≤3－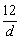

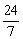∵－＜d＜－3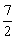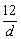，∴＜－＜4，得5.5＜k＜7.

因为k是正整数，所以k=6，即在S1，S2，…，S12中，S6最大.

解法二：由d＜0得a1>a2>…>a12>a13，

因此若在1≤k≤12中有自然数k，使得ak≥0，且ak+1＜0，则Sk是S1，S2，…，S12中的最大值。又2a7=a1+a13=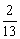S13＜0，  ∴a7＜0，     a7+a6=a1+a12=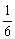S12>0，   ∴a6≥－a7>0

故在S1，S2，…，S12中S6最大.

解法三：依题意得：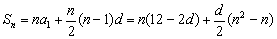

最小时，Sn最大；

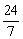∵－＜d＜－3，  ∴6＜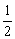

上一页  [1] [2] [3] [4] [5]  下一页

你可能还感兴趣的《2017高考数学复习：数列（二）》相关文章

• 2017高考数学复习：数列（二）
• › 2017马年春节对联：春节七字春联齐齐看
• › 2017年感恩节是几月几日
• › 2017年中秋节活动方案
• › 2017中秋节活动方案汇总
• › 2017中秋节活动方案
• › 2017麓山国际实验学校新高一入学安排
• › 2017明德中学秋季高一新生入学须知
• › 2017长沙市实验中学高中新生入学安排
• › 2017广益实验中学高一新生入学须知
• › 2017长郡湘府班高一新学生报到须知
• › 2017长郡中学高一新生报到须知
• › 2017雅礼中学高中新生入学须知
• 在百度中搜索相关文章：2017高考数学复习：数列（二）
• 在谷歌中搜索相关文章：2017高考数学复习：数列（二）
• 在soso中搜索相关文章：2017高考数学复习：数列（二）
• 在搜狗中搜索相关文章：2017高考数学复习：数列（二）