2013高考数学复习：数列（二）
【知识图解】 
【方法点拨】
1．学会从特殊到一般的观察、分析、思考，学会归纳、猜想、验证．
2．强化基本量思想，并在确定基本量时注重设变量的技巧与解方程组的技巧．
3．在重点掌握等差、等比数列的通项公式、求和公式、中项等基础知识的同时，会针对可化为等差（比）数列的比较简单的数列进行化归与转化．
4．一些简单特殊数列的求通项与求和问题，应注重通性通法的复习．如错位相减法、迭加法、迭乘法等．
5．增强用数学的意识，会针对有关应用问题，建立数学模型，并求出其解．
第2课 等差、等比数列
【考点导读】
1.掌握等差、等比数列的通项公式、前
项和公式，能运用公式解决一些简单的问题；
2. 理解等差、等比数列的性质，了解等差、等比数列与函数之间的关系；
3.注意函数与方程思想方法的运用。
【基础练习】
1．在等差数列{an}中，已知a5＝10，a12＝31，首项a1= -2 ，公差d= 3 。
2．一个等比数列的第3项与第4项分别是12与18，则它的第1项是
，第2项是 8 。
3．设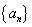
是公差为正数的等差数列，若
，
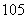，则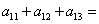
。
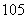4．公差不为0的等差数列{an}中，a2，a3，a6依次成等比数列，则公比等于 3 。
【范例导析】
例1．（1）若一个等差数列前3项的和为34，最后3项的和为146，且所有项的和为390，则这个数列有
13 项。
（2）设数列{an}是递增等差数列，前三项的和为12，前三项的积为48，则它的首项是 2 。
解：（1）答案：13
法1：设这个数列有n项
∵
∴
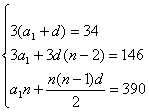
∴n＝13
法2：设这个数列有n项
∵
∴
∴
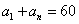
又
- 2017高考数学复习：数列（二）
- › 2017马年春节对联：春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章：2017高考数学复习：数列（二）
- 在谷歌中搜索相关文章：2017高考数学复习：数列（二）
- 在soso中搜索相关文章：2017高考数学复习：数列（二）
- 在搜狗中搜索相关文章：2017高考数学复习：数列（二）