的首项
，
（
）。
（1）证明：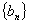
从第2项起是以2为公比的等比数列；
（2）设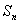
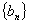为数列的前n项和，且
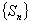是等比数列，求实数
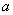的值。
分析：第（1）问用定义证明，进一步第（2）问也可以求出。
解：（1）∵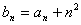
∴
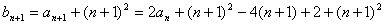
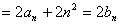(n≥2)
由
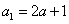得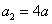
，
，∵
，∴
，
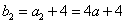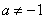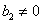即
从第2项起是以2为公比的等比数列。
（2）
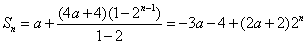
当n≥2时，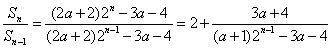
∵
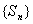是等比数列， ∴
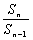(n≥2)是常数， ∴3a+4=0，即
。
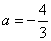点评：本题考查了用定义证明等比数列，分类讨论的数学思想，有一定的综合性。
www.kuaixue5.com【反馈演练】
1．已知等差数列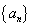
中，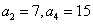
，则前10项的和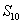
Tag:高考数学复习，高考数学复习大全，高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
- 2017高考数学复习：数列（二）
- › 2017马年春节对联：春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章：2017高考数学复习：数列（二）
- 在谷歌中搜索相关文章：2017高考数学复习：数列（二）
- 在soso中搜索相关文章：2017高考数学复习：数列（二）
- 在搜狗中搜索相关文章：2017高考数学复习：数列（二）