18．如图，平行于x轴的直线AC分别交抛物线y1=x2（x≥0）与y2=x2/3（x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则= .
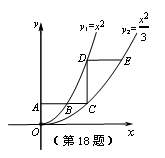
三、解答题（本大题共有9小题，共78分）
19．计算（每小题4分，共8分）
（1）(√27－√12＋√45)×√(1/3)； （2）(√2－√3)2＋√18÷√3．
20．解方程（每小题4分，共8分）
（1） x2－4x＋2＝0； （2）2(x－3)＝3x(x－3)．
21．（本题满分6分）将背面完全相同，正面上分别写有数字1、2、3、4的四张卡片混合后，小明从中随机地抽取一张，把卡片上的数字作为被减数，将形状、大小完全相同，分别标有数字1、2、3的三个小球混合后，小华从中随机地抽取一个，把小球上的数字作为减数，然后计算出这两个数的差．
（1）请你用画树状图或列表的方法，求这两数差为0的概率；
（2）小明与小华做游戏，规则是：若这两数的差为非负数，则小明赢；否则，小华赢.你认为该游戏公平吗？请说明理由.如果不公平，请你修改游戏规则，使游戏公平．
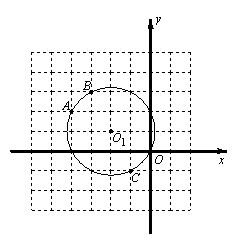22.（本题6分）已知⊙O1经过A（－4，2）、B（－3，3）、C（－1，－1）、O（0，0）四点，一次函数y＝－x－2的图象是直线l，直线l与y轴交于点D．
（1）在右边的平面直角坐标系中画出直线l，则直线l与⊙O1的交点坐标为 ；
（2）若⊙O1上存在点P，使得△APD为等腰三角形，则这样的点P有 个，试写出其中一个点P坐标为 ．
23．（本题8分）如图，四边形ABCD中，AB∥CD，AC平分∠BAD，过C作CE∥AD交AB于E．
（1）求证：四边形AECD是菱形；
（2）若点E是AB的中点，试判断△ABC的形状，并说明理由．
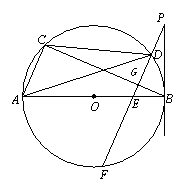24．（本题10分）如图，AB是⊙O的直径，C、D在⊙O上，连结BC，过D作PF∥AC交AB于E，交⊙O于F，交BC于点G，且∠BPF＝∠ADC．
（1）判断直线BP与⊙O的位置关系，并说明理由；
（2）若⊙O的半径为，AC＝2，BE＝1，求BP的长．
www.kuaixue5.com
25．（本题10分）某商场购进一批单价为16元的日用品.若按每件23元的价格销售，每月能卖出270件；若按每件28元的价格销售，每月能卖出120件；若规定售价不得低于23元，假定每月销售件数y(件)与价格x（元/件）之间满足一次函数.
（1）试求y与x之间的函数关系式．
（2）在商品不积压且不考虑其他因素的条件下，销售价格定为多少时，才能使每月的毛利润w最大？每月的最大毛利润为多少？
（3）若要使某月的毛利润为1800元，售价应定为多少元？
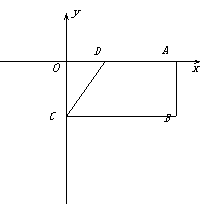26．(本题10分)如图，在矩形OABC中，OA＝8，OC＝4，OA、OC分别在x轴与y轴上，D为OA上一点，且CD＝AD．
（1）求点D的坐标；
（2）若经过B、C、D三点的抛物线与x轴的另一个交点为E，请直接写出点E的坐标；
（3）在（2）中的抛物线上位于x轴上方的部分，是否存在一点P，使△PBC的面积等于梯形DCBE的面积？若存在，求出点P的坐标，若不存在，请说明理由．
27．（本题12分）如图，抛物线y＝x2－x－12与x轴交于A、C两点，与y轴交于B点．
（1）求△AOB的外接圆的面积；
（2）若动点P从点A出发，以每秒2个单位沿射线AC方向运动；同时，点Q从点B出发，以每秒1个单位沿射线BA方向运动，当点P到达点C处时，两点同时停止运动。问当t为何值时，以A、P、Q为顶点的三角形与△OAB相似？
（3）若M为线段AB上一个动点，过点M作MN平行于y轴交抛物线于点N．
①是否存在这样的点M，使得四边形OMNB恰为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．
②当点M运动到何处时，四边形CBNA的面积最大？求出此时点M的坐标及四边形CBAN面积的最大值．
- 无锡市初三上册数学期末试卷及答案
- › 无锡市初三上册数学期末试卷及答案
- 在百度中搜索相关文章：无锡市初三上册数学期末试卷及答案
- 在谷歌中搜索相关文章：无锡市初三上册数学期末试卷及答案
- 在soso中搜索相关文章：无锡市初三上册数学期末试卷及答案
- 在搜狗中搜索相关文章：无锡市初三上册数学期末试卷及答案