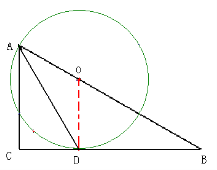
判断结果：BC是⊙O的切线。连结OD。
∵AD平分∠BAC ∴∠DAC=∠DAB
∵OA=OD ∴∠ODA=∠DAB
∴∠DAC=∠ODA ∴OD∥AC ∴∠ODB=∠C
∵∠C=90º ∴∠ODB=90º 即：OD⊥BC
∵OD是⊙O的半径 ∴ BC是⊙O的切线。
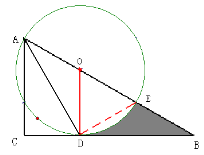
(2) 如图，连结DE。
设⊙O的半径为r，则OB=6-r，
在Rt△ODB中，∠ODB=90º，
∴0B2=OD2+BD2 即：(6-r)2= r2+(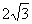
)2
∴r=2 ∴OB=4 ∴∠OBD=30º，∠DOB=60º
∵△ODB的面积为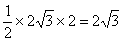
，扇形ODE的面积为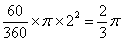
∴阴影部分的面积为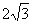
—
。
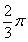25. 解：
(1)300，36。
(2)喜欢足球的有300－120－60－30＝90人，所以据此将条形图补充完整
(3)在参加调查的学生中，喜欢篮球的有120人，占120÷300＝40%，所以该校2000名学生中，估计喜欢“篮球”的学生共有2000×40%=800（人）。
26.：（1）连接OE，
∵AE平分∠BAF，
∴∠BAE=∠DAE．
∵OE=OA，
∴∠BAE=∠OEA．
∴∠OEA=∠DAE．
∴OE∥AD．
∵AD⊥CD，
∴OE⊥CD．
∴CD是⊙O的切线．
(2)AE=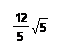
27. 解：（1）D点的坐标为（-2，3）
（2）设一次函数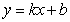
把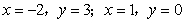
代入上式
得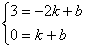
解得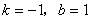
∴一次函数的关系式为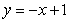
（3）当
或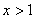
时，一次函数的值大于二次函数的值
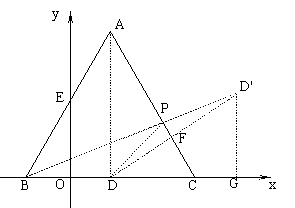
28. 解：（1）连结AD，不难求得A（1，2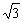
）
- 九年级第一学期数学期末联考试卷及答案
- › 朝阳区九年级第一学期期末试卷
- › 海淀区九年级第一学期期中化学试卷
- › 海淀区九年级第一学期期中数学试题及答案
- › 海淀区九年级第一学期期中物理试题及答案
- › 九年级第一学期数学期末试卷及答案
- › 九年级第一学期数学期末联考试卷及答案
- 在百度中搜索相关文章：九年级第一学期数学期末联考试卷及答案
- 在谷歌中搜索相关文章：九年级第一学期数学期末联考试卷及答案
- 在soso中搜索相关文章：九年级第一学期数学期末联考试卷及答案
- 在搜狗中搜索相关文章：九年级第一学期数学期末联考试卷及答案