，∵A，B两点分别l1和l2上，∴
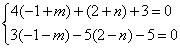，消去常数项得－3m＝n，所以k＝－3，
从而直线l的方程为3x＋y＋1＝0.
解法三 设l1、l2与l的交点分别为A，B，则l1关于点P（－1，2）对称的直线m过点B，利用对称关系可求得m的方程为4x＋y＋1＝0，因为直线l过点B，故直线l的方程可设为3x－5y－5＋λ（4x＋y＋1）＝0.由于直线l点P（－1，2），所以可求得λ＝－18，从而l的方程为3x－5y－5－18（4x＋y＋1）＝0，即3x＋y＋1＝0.
点评 本题主要复习有关线段中点的几种解法，本题也可以先设直线方程，然后求交点，再根据中点坐标求出直线l的斜率，但这种解法思路清晰，计算量大，解法一和解法二灵活运用中点坐标公式，使计算简化，对解法二还可以用来求已知中点坐标的圆锥曲线的弦所在直线方程，解法三是利用直线系方程求解，对学生的思维层次要求较高。
【反馈练习】
1.已知下列四个命题①经过定点P0(x0，y0)的直线都可以用方程y-y0＝k(x-x0)表示；②经过任意两个不同点P1(x1，y1)、P2(x2，y2)的直线都可以用方程(y-y1)(x2-x1)＝(x-x1)(y2-y1)表示；③不经过原点的直线都可以用方程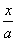
+
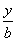＝1表示；④经过定点A(0，b)的直线都可以用方程y＝kx+b表示，其中正确的是①③④
2.设直线l的方程为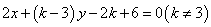
，当直线l的斜率为-1时，k值为__5__，当直线l 在x轴、y轴上截距之和等于0时，k值为1或3
3.设直线 ax+by+c=0的倾斜角为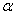
，且sin
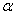+cos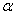=0，则a，b满足的关系式为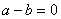
4.若直线l：y＝kx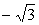
与直线2x＋3y－6＝0的交点位于第一象限，则直线l的倾斜角的取值范围是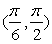
5.若直线4x-3y-12＝0被两坐标轴截得的线段长为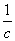
，则c的值为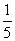
6．若直线(m2─1)x─y─2m+1=0不经过第一象限，则实数m的取值范围是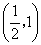
7.已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P（2，3），求过两点Q1（a1，b1）、Q2（a2，b2）（a1≠a2）的直线方程
分析：利用点斜式或直线与方程的概念进行解答
解：∵P（2，3）在已知直线上，∴ 2a1+3b1+1=0，2a2+3b2+1=0
∴2（a1－a2）+3（b1－b2）=0，即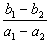
=－
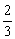∴所求直线方程为y－b1=－
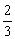（x－a1）
∴2x+3y－（2a1+3b1）=0，即2x+3y+1=0
点拨：1.由已知求斜率; 2.运用了整体代入的思想，方法巧妙.
8.一条直线经过点P（3，2），并且分别满足下列条件，求直线方程：
（1）倾斜角是直线x－4y+3=0的倾斜角的2倍；
（2）与x、y轴的正半轴交于A、B两点，且△AOB的面积最小（O为坐标原点）
- 2017高考数学复习：直线和圆的方程（一）
- › 2017马年春节对联：春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章：2017高考数学复习：直线和圆的方程（一）
- 在谷歌中搜索相关文章：2017高考数学复习：直线和圆的方程（一）
- 在soso中搜索相关文章：2017高考数学复习：直线和圆的方程（一）
- 在搜狗中搜索相关文章：2017高考数学复习：直线和圆的方程（一）