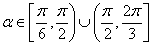
∴
故综合①、②得，直线AB的倾斜角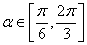
点拨：本题容易忽视对分母等于0和斜率不存在情况的讨论.
例2.直线l过点P(2，1)，且分别交x轴、y轴的正半轴于点A、B、O为坐标原点.
(1)当△AOB的面积最小时，求直线l的方程;
(2)当|PA|·|PB|取最小值时，求直线l的方程.
分析： 引进合适的变量，建立相应的目标函数，通过寻找函数最值的取得条件来求l的方程.
解 （1）设直线l的方程为y-1=k(x-2)，则点A(2-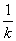
，0)，B(0，1-2k)，且2-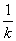>0， 1-2k>0，即k<0.
△AOB的面积S=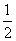
(1-2k)(2-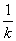)=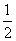[(-4k)+
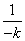+4]≥4，当-4k=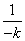，即k=
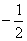时， △AOB的面积有最小值4，则所求直线方程是x+2y-4=0.
(2)解法一:由题设，可令直线方程l为y-1=k(x-2).
分别令y=0和x=0，得A(2-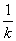，0)，B(0，1-2k)，
∴|PA|·|PB|=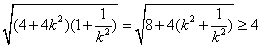
，当且仅当k2=1，即k=±1时， |PA|·|PB|取得最小值4.又k<0， ∴k=-1，这是直线l的方程是x+y-3=0.
解法二:如下图，设∠BAO=θ，由题意得θ∈(0，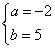
)，且|PA|·|PB|=
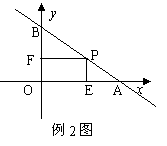
当且仅当θ=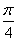
时， |PA|·|PB|取得最小值4，此时直线l的斜率为-1， 直线l的方程是x+y-3=0.
点评 ①求直线方程的基本方法包括利用条件直接求直线的基本量和利用待定系数法求直线的基本量.②在研究最值问题时，可以从几何图形开始，找到取最值时的情形，也可以从代数角度出发，构建目标函数，利用函数的单调性或基本不等式等知识来求最值.
www.kuaixue5.com例3.直线l被两条直线l1：4x＋y＋3＝0和l2：3x－5y－5＝0截得的线段中点为P（－1，2）.求直线l的方程.
分析 本题关键是如何使用好中点坐标，对问题进行适当转化.
解：解法一 设直线l交l1于A（a，b），则点（－2－a，4－b）必在l2，所以有
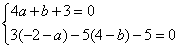，解得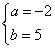
直线l过A(-2，5)，P(-1，2)，它的方程是3x＋y＋1＝0.
解法二 由已知可设直线l与l1的交点为A（－1＋m，2＋n），则直线l与l2的交点为B（－1－m，2－n），且l的斜率k＝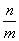
- 2017高考数学复习：直线和圆的方程（一）
- › 2017马年春节对联：春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章：2017高考数学复习：直线和圆的方程（一）
- 在谷歌中搜索相关文章：2017高考数学复习：直线和圆的方程（一）
- 在soso中搜索相关文章：2017高考数学复习：直线和圆的方程（一）
- 在搜狗中搜索相关文章：2017高考数学复习：直线和圆的方程（一）