5的正方形网格中,每个小正方形的边长均为1,M、N是两个格点,在格点上是否存在点P,使△PMN的面积等于1?若存在,在图中标出它的位置;若不存在,请说明理由.
 四、(本大题共20分,每小题5分)解答题:
四、(本大题共20分,每小题5分)解答题:
19.(本小题5分)如图,△ABC中,∠A=30°,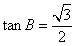 ,
,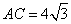 .求AB的长.
.求AB的长.
(第19题图)
www.kuaixue5.com
20.(本小题5分)在平面直角坐标系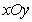 中,直线
中,直线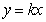 沿
沿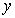 轴向上平移3个单位长度后与x轴交于A
轴向上平移3个单位长度后与x轴交于A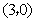 ,与
,与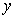 轴交于点
轴交于点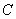 .抛物线
.抛物线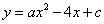 过点A,C,求直线
过点A,C,求直线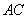 及抛物线的解析式.
及抛物线的解析式.
 21.(本小题5分)已知反比例函数
21.(本小题5分)已知反比例函数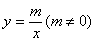 的图象经过点A(
的图象经过点A( ,6).
,6).
(1)求m的值;
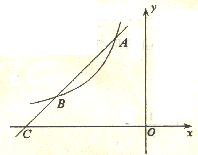
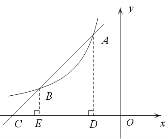
(2)如图,过点A作直线AC与函数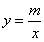 的图象交于点B,与x轴交于点C,且
的图象交于点B,与x轴交于点C,且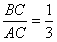 ,求点B的坐标.
,求点B的坐标.
(第21题图)
22.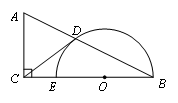 (本小题5分)如图,在△ABC中,∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边和BC边分别交于点D、点E,连接CD,且CD=CA,BD=
(本小题5分)如图,在△ABC中,∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边和BC边分别交于点D、点E,连接CD,且CD=CA,BD=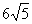 ,tan∠ADC=2.
,tan∠ADC=2.
(1)求证:CD是半⊙O的切线;
(2)求半⊙O的直径;
(3)求AD的长.
www.kuaixue5.com五、(本大题共23分,其中第23题6分,第24题8分,第25题9分)
23.(本小题6分)已知抛物线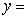
 与y轴交于点A,与x轴交于B、C两点(C在B的左边).
与y轴交于点A,与x轴交于B、C两点(C在B的左边).
(1)过A、O、B三点作⊙M,求⊙M的半径;
(2)点P为弧OAB上的动点,当点P运动到何位置时△OPB的面积最大?求出此时点P的坐标及△OPB的最大面积.
24.(本题8分)已知关于x的一元二次方程kx2+(3k+1)x+2k+1=0
(1)求证:该方程必有两个实数根.
(2)若该方程只有整数根,求k的整数值
(3)在(2)的条件下,在平面直角坐标系中,若二次函数y=(k+1)x2+3x+m与x轴有两个不同的交点A和B(A在B左侧),并且满足OA=2·OB,求m的非负整数值.
25.(本小题9分)如图,在直角坐标系中,以点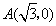 为圆心,以
为圆心,以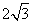 为半径的⊙A与
为半径的⊙A与 轴相交于点
轴相交于点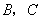 ,与
,与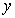 轴相交于点
轴相交于点 .
.
(1)若抛物线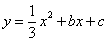 经过
经过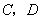 两点,求抛物线的解析式,并判断点
两点,求抛物线的解析式,并判断点 是否在该抛物线上;
是否在该抛物线上;
(2)在(1)中的抛物线的对称轴上求一点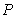 ,使得
,使得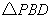 的周长最小;
的周长最小;
(3)设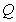 为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点
为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点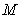 ,使得以B、C、Q、M为顶点的四边形是平行四边形?∠若存在,求出点
,使得以B、C、Q、M为顶点的四边形是平行四边形?∠若存在,求出点
 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
参考答案:
一、(本题共32分,每小题4分)选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | D | C | A | B | C | D | B | C |
二、(本大题16分,每小题4分)填空题:
9. 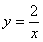 ; 10.
; 10. 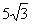 ; 11. 6π; 12.(36,0).
; 11. 6π; 12.(36,0).
三、(本大题共20分,每小题5分)解答题:
13.解:原式= -------------------------------------4分
-------------------------------------4分
=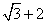 --------------------------------------5分
--------------------------------------5分
14.解:(1) 如图
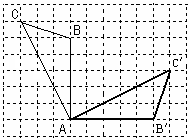
∴△AB′C′ 为所求 --------------------------------3分
(2) 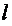 BB
BB =
=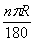 -------------------------------------------------4分
-------------------------------------------------4分
=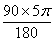
= -----------------------------------5分
-----------------------------------5分
15. 解:游戏公平. --------------------------------------------------1分
列表或画树状图正确. -------------------------------------------------2分
∵ P(两张卡片上的数字之和为奇数)=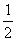 ,------------------------3分
,------------------------3分
P(两张卡片上的数字之和为偶数)=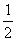 ,--------------------------------------4分
,--------------------------------------4分
∴ P(两张卡片上的数字之和为奇数)= P(两张卡片上的数字之和为偶数).
∴ 这个游戏公平. ------------------------------------------------------5分
16.解:(1)由图可知:A(-2,1),B(1,-2) ------------------- 1分
∵反比例函数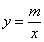 的图象过点
的图象过点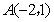
∴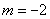 , ∴
, ∴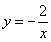 ----------------------------------------2分
----------------------------------------2分
∵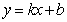 过
过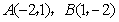
∴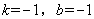
∴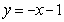 ---------------------------------------------------------4分
---------------------------------------------------------4分
(2)-2<x<0或x>1 -------------------------------------- 5分
 17.解:联结AC
17.解:联结AC
∵AD=BD ∴∠ACD=∠ABD=∠BAD----------1分
∵∠ADP=∠ADC
∴△ADC∽△PDA --------------------2分
∴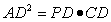 ---------------------------------3分
---------------------------------3分
设PD=x,∵AD=4,PC=6
则有:16=x(x+6) 解得x=2或x= -8(舍去-8)---4分
∴CD=2+6=8
∴CD的长为8 ------------------------------------------5分
18.

四、(本大题共20分,每小题5分)解答题:
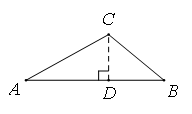
19.解:过点C作CD⊥AB于点D ----------1分
∵∠A=30°且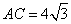
∴CD=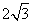 ,cosA=
,cosA=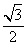 ------------2分
------------2分
∴AD=6 -----------------------------------------3分
∵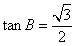
∴BD=4 ---------------------------------------4分
∴AB=4+6=10 ----------------------------------------5分
20.解:将直线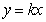 沿
沿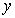 轴向上平移3个单位长度后得到
轴向上平移3个单位长度后得到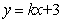 ------1分
------1分
∵平移后的直线过点A(3,0)
∴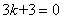
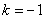
∴直线AC的解析式为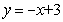 -------------------------2分
-------------------------2分
∵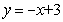 与
与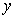 轴交于点
轴交于点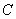
∴C(0,3) ------------------------3分
∵抛物线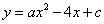 过点A(3,0),C(0, 3)
过点A(3,0),C(0, 3)
∴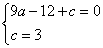
解得: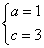 --------------------------4分
--------------------------4分
∴抛物线的解析式为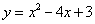 ----------------------------------------5分
----------------------------------------5分
21.解:(1) ∵反比例函数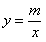 (m≠0)的图象经过点A(-2,6),
(m≠0)的图象经过点A(-2,6),
∴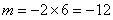 ∴m的值为-12.----------1分
∴m的值为-12.----------1分
 (2) 由(1)得反比例函数的解析式为
(2) 由(1)得反比例函数的解析式为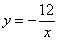 .
.
过点A作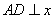 轴于点
轴于点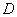 ,过点B作
,过点B作 轴于点
轴于点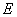 ,
,
∴Rt△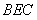 ∽Rt△
∽Rt△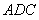 .--------------------------2分
.--------------------------2分
∴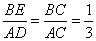 .
.
∵ ,
,
∴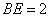 . -------------------------------------------------3分
. -------------------------------------------------3分
∴点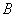 的纵坐标为2. --------------------------------------------------4分
的纵坐标为2. --------------------------------------------------4分
又点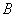 在反比例函数
在反比例函数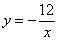 的图象上,
的图象上,
∴点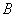 的横坐标为x= -6,
的横坐标为x= -6,
即点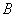 的坐标为(-6,2). ------------------------------------------------5分
的坐标为(-6,2). ------------------------------------------------5分

22.(1)证明:联结OD ∵CD=CA,OB=OD
∴∠CAD=∠A,∠ODB=∠OBD
∵∠ACB=90°,∴∠A+∠OBD=90°
∴∠CDA+∠ODB=90°
∴∠CDO=90°
∴CD⊥OD ----------------------------1分
∵点D在半⊙O上,∴CD是半⊙O的切线 ---------------------------2分
 (2)联结DE
(2)联结DE
∵BE是半⊙O的直径,
∴∠EDB=90° ----------------------3分
∵tan∠ADC=2,∠CAD=∠A
∴tanA=2,∴tan∠EBD=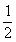
在△EDB中,∠EDB=90°,BD=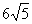 ,tan∠EBD=
,tan∠EBD=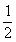
∴BE=15,即半⊙O的直径是15 ---------------------------4分
(3)在△ABC中,∠ACB=90°,tan∠ABC=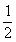
设AC= x,则CD=x,BC=2 x
∵∠CBD+∠A=90°,∠ADC+∠CDE=90°
∠CDE=∠CBD ∴△CDE∽△CBD
∴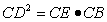 ∴CE=0.5x
∴CE=0.5x
∴△BDE∽△BCA ,DE:AC=BD:BC
∴3 :x=6
:x=6 :(15+0.5x), ∴x=10
:(15+0.5x), ∴x=10
在△ABC中,∠ACB=90°AC=10,BC=20
∴AB=10 , ∴AD=4
, ∴AD=4 ------------------- 5分
------------------- 5分
23.解:(1)由题意可得:A(0,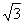 ),B(3,0)
),B(3,0)
∴OA=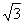 , OB=3---------------------1分
, OB=3---------------------1分
联结AB,∵∠AOB=90°,
∴ AB为⊙M的直径 -----------------------------2分
∴AB=2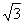
∴⊙M的半径为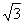 ---------------------------------------3分
---------------------------------------3分
(2)在△AOB中,∵OA=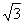 , OB=3,∠AOB=90°
, OB=3,∠AOB=90°
∴∠OAB =60°
∵点P为弧OAB上的动点
∴∠OPB =60° -------------------------------------------------4分
∵OB=3是定值,要使△OPB面积最大,只要使OB边上的高最大,
即点P到OB边的距离最大
∴点P为为弧OAB的中点,此时为△OPB为等边三角形
∴P(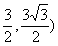 ,△OPB的最大面积为
,△OPB的最大面积为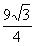 -------------------------------------6分
-------------------------------------6分
24.(1)证明:△=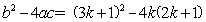
=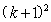 ≥0
≥0
∴该方程必有两个实数根. --------------------------1分
(2)解: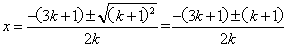
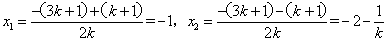 -----------3分
-----------3分
∵方程只有整数根,
∴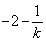 应为整数,即
应为整数,即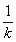 应为整数
应为整数
∵k为整数
∴k=±1 -------------------4分
(3)根据题意,k+1≠0,即k≠-1, ------------------5分
∴k=1,此时, 二次函数为y=2x2+3x+m
∵二次函数与x轴有两个不同的交点A和B(A在B左侧)
∴△= >0,m<
>0,m<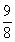 ,
,
∵m为非负整数
∴m=0,1 ---------------------------------------------------6分
当m=0时,二次函数为y=2x2+3x,此时A(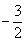 ,0),B(0,0)
,0),B(0,0)
不满足OA=2·OB. ---------------------------------7分
当m=1时,二次函数为y=2x2+3x+1,此时A(-1,0),B(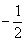 ,0)
,0)
满足OA=2·OB.
∴k=1 --------------------------------8分
25.解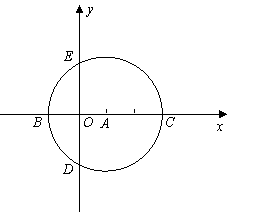 :(1)∵
:(1)∵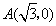 ,⊙A的半径为
,⊙A的半径为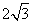
∴OA=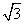 ,AD=
,AD=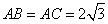
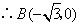 ,
,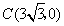 -------------------1分
-------------------1分
在 中,
中,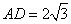 ,
,
∴OD=3,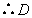 的坐标为
的坐标为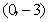 ------------2分
------------2分
∵抛物线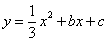 过
过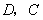 两点,
两点,
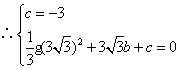
∴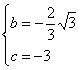
 所求抛物线的解析式为:
所求抛物线的解析式为: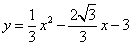 -----------------------------3分
-----------------------------3分
当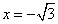 时,
时,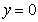
 点
点 在抛物线上 -------------------------------------4分
在抛物线上 -------------------------------------4分
(2)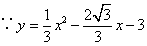
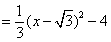
 抛物线
抛物线 的对称轴方程为
的对称轴方程为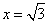
在抛物线的对称轴上存在点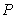 ,使
,使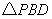 的周长最小.
的周长最小.
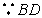 的长为定值
的长为定值  要使
要使 周长最小只需
周长最小只需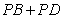 最小.
最小.
连结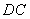 ,则
,则 与对称轴的交点即为使
与对称轴的交点即为使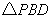 周长最小的点.
周长最小的点.
∵直线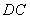 的解析式为
的解析式为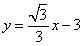 ----------------------------------------5分
----------------------------------------5分
当x=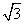 时,y=-2,
时,y=-2,
∴所求点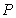 的坐标为
的坐标为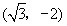 ------------------------------------------6分
------------------------------------------6分
(3)在抛物线上存在点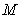 ,使得以B、C、Q、M为顶点的四边形是平行四边形.
,使得以B、C、Q、M为顶点的四边形是平行四边形.
∵BC=4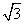
① 当BC为平行四边形的边,且点M在抛物线对称轴的左侧时,
所求M点的坐标是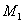 (-3
(-3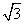 ,12) --------------------------------------------7分
,12) --------------------------------------------7分
②当BC为平行四边形的边,且点M在抛物线对称轴的右侧时,
所求M点的坐标是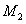 (5
(5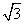 ,12)--------------------------------------------8分
,12)--------------------------------------------8分
③当BC为平行四边形的对角线时,所求M点的坐标是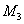 (
(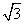 ,4)-----9分
,4)-----9分
综上所述:在抛物线上存在点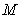 ,使得以B、C、Q、M为顶点的四边形是平行四边形,且所求M的坐标为
,使得以B、C、Q、M为顶点的四边形是平行四边形,且所求M的坐标为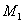 (-3
(-3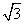 ,12)、
,12)、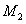 (5
(5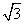 ,12)、
,12)、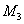 (
(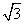 ,4).
,4).
- 房山区初三上册数学期末试卷及答案
- › 房山区初三上册数学期末试卷及答案
- › 北京房山区初三语文上期末试卷及答案
- 在百度中搜索相关文章:房山区初三上册数学期末试卷及答案
- 在谷歌中搜索相关文章:房山区初三上册数学期末试卷及答案
- 在soso中搜索相关文章:房山区初三上册数学期末试卷及答案
- 在搜狗中搜索相关文章:房山区初三上册数学期末试卷及答案
