（1）∠APC=∠PAB+∠PCD；
证明：过点P作AB∥PF，
∵AB∥PF，∴AB∥CD∥PF，
∴
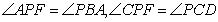（两直线平行，内错角相等），
∴∠APC=∠PAB+∠PCD．
（2）∠APC+∠PAB+∠PCD=360°；
（3）∠APC=∠PAB-∠PCD；
（4）∠PCD=∠PAB+∠APC.
2．解：（1）如图，当动点P落在第②部分时，∠APB=360°-（∠PAC+∠PBD）；
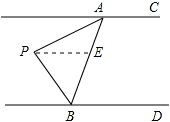
（2）当动点P落在第③部分时，∠PAC=∠APB+∠PBD；
当动点P落在第部分时，∠PAC =∠APB+∠PBD．
证明：如图，∵∠PAC=∠AEB，∠AEB=∠PBD+∠APB，
∴∠PAC= ∠APB +∠PBD．
7.5 三角形内角和定理
专题 与三角形内角和外角有关的探究题
1．如下几个图形是五角星和它的变形．
（1）图（1）中是一个五角星，求∠A+∠B+∠C+∠D+∠E；
（2）图（2）中的点A向下移到BE上时，五个角的和（即∠CAD+∠B+∠C+∠D+∠E）有无变化？说明你的结论的正确性；
（3）把图（2）中的点C向上移到BD上时，如图（3）所示，五个角的和（即∠CAD+∠B+∠ACE+∠D+∠E）有无变化？说明你的结论的正确性．
2．认真阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题.
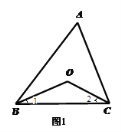
探究1：如图1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+
，理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线，
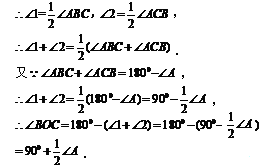
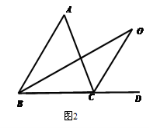
探究2：如图2，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由.
探究3：如图3，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（只写结论，不需证明）
答案：
1．解：（1）如图，连接CD．
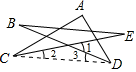在△ACD中，根据三角形内角和定理，得出∠A+∠2+∠3+∠ACE+∠ADB=180°．
∵∠1=∠B+∠E=∠2+∠3，
∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠B+∠E+∠ACE+∠ADB=∠A+∠2+∠3+∠ACE+∠ADB=180°.
（2）无变化．
根据平角的定义，得出∠BAC+∠CAD+∠DAE=180°．
∵∠BAC=∠C+∠E，∠EAD=∠B+∠D，w W w .X k b 1.c O m
∴∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠DAE=180°；
（3）无变化．
∵∠ACB=∠CAD+∠D，∠ECD=∠B+∠E，
∴∠CAD+∠B+∠ACE+∠D+∠E=∠ACB+∠ACE+∠ECD=180°．
2．解：（1）探究2的结论：∠BOC=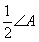
.
理由如下：
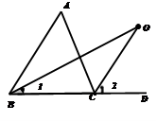
∵ BO和CO分别是∠ABC和∠ACD的角平分线，所以
- 初二上册平行线的证明练习题及答案
- › 初二上册牛津英语期末试卷及答案
- › 南通市初二上册英语期末试卷及答案
- › 镇江六校初二上册英语期末试卷及答案
- › 2014外研版初二上册英语期末试卷及答案
- › 建阳市初二上册英语期末试卷及答案
- › 镇江市初二上册英语期末试卷及答案
- › 2014天津初二上册英语期末试卷及答案
- › 樟树市初二上册英语期末试卷及答案
- › 建平县初二上册英语期末试卷及答案
- › 姜堰市初二上册英语期末试卷及答案
- › 瓜州二中初二上册英语期末试卷及答案
- › 初二上册勾股定理单元检测卷及答案
- 在百度中搜索相关文章：初二上册平行线的证明练习题及答案
- 在谷歌中搜索相关文章：初二上册平行线的证明练习题及答案
- 在soso中搜索相关文章：初二上册平行线的证明练习题及答案
- 在搜狗中搜索相关文章：初二上册平行线的证明练习题及答案