有最小值
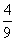 .
.
(2)设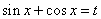
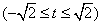 ,则
,则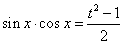 ,则
,则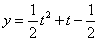 ,当
,当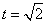 时,
时,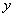 有最大值为
有最大值为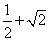 .
.
点评:第(1)小题利用消元法,第(2)小题利用换元法最终都转化为二次函数求最值问题;但要注意变量的取值范围.
例2.求函数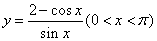 的最小值.
的最小值.
分析:利用函数的有界性求解.
解法一:原式可化为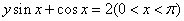 ,得
,得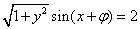 ,即
,即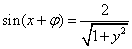 ,
,
故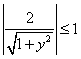 ,解得
,解得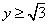 或
或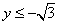 (舍),所以
(舍),所以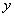 的最小值为
的最小值为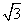 .
.
解法二: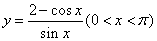 表示的是点
表示的是点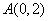 与
与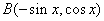 连线的斜率,其中点B在左半圆
连线的斜率,其中点B在左半圆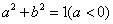 上,由图像知,当AB与半圆相切时,
上,由图像知,当AB与半圆相切时,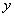 最小,此时
最小,此时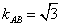 ,所以
,所以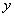 的最小值为
的最小值为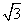
Tag:高考数学复习,高考数学复习大全,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
- 2017高考数学复习:三角函数(三)
- › 2017马年春节对联:春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章:2017高考数学复习:三角函数(三)
- 在谷歌中搜索相关文章:2017高考数学复习:三角函数(三)
- 在soso中搜索相关文章:2017高考数学复习:三角函数(三)
- 在搜狗中搜索相关文章:2017高考数学复习:三角函数(三)
