相交线与平行线知识点:平行线的性质
5.3平行线的性质
1、平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补。
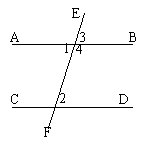
几何符号语言:
∵AB∥CD
∴∠1=∠2(两直线平行,内错角相等)
∵AB∥CD
∴∠3=∠2(两直线平行,同位角相等)
∵AB∥CD
∴∠4+∠2=180°(两直线平行,同旁内角互补)
2、两条平行线的距离
如图,直线AB∥CD,EF⊥AB于E,EF⊥CD于F,则称线段EF的长度为两平行线AB与CD间的距离。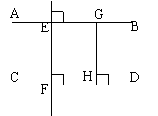

注意:直线AB∥CD,在直线AB上任取一点G,过点G作CD的垂线段GH,则垂线段GH的长度也就是直线AB与CD间的距离。
www.kuaixue5.com3、命题:
⑴命题的概念:
判断一件事情的语句,叫做命题。
⑵命题的组成
每个命题都是题设、结论两部分组成。题设是已知事项;结论是由已知事项推出的事项。命题常写成“如果……,那么……”的形式。具有这种形式的命题中,用“如果”开始的部分是题设,用“那么”开始的部分是结论。
有些命题,没有写成“如果……,那么……”的形式,题设和结论不明显。对于这样的命题,要经过分析才能找出题设和结论,也可以将它们改写成“如果……,那么……”的形式。
注意:命题的题设(条件)部分,有时也可用“已知……”或者“若……”等形式表述;命题的结论部分,有时也可用“求证……”或“则……”等形式表述。
4、平行线的性质与判定
①平行线的性质与判定是互逆的关系
两直线平行  同位角相等;
同位角相等;
两直线平行 内错角相等;
两直线平行 同旁内角互补。
其中,由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质。

典型例题:已知∠1=∠B,求证:∠2=∠C
证明:
∵∠1=∠B(已知)
∴DE∥BC(同位角相等,两直线平行)
∴∠2=∠C(两直线平行同位角相等)
注意,在了DE∥BC,不需要再写一次了,得到了DE∥BC,这可以把它当作条件来用了。
典型例题:如图,AB∥DF,DE∥BC,∠1=65°,求∠2、∠3的度数。
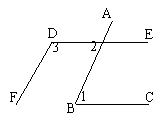
解答:
∵DE∥BC(已知)
∴∠2=∠1=65°(两直线平行,内错角相等)
∵AB∥DF(已知)
∴AB∥DF(已知)
∴∠3+∠2=180°(两直线平行,同旁内角互补)
∴∠3=180°-∠2=180°-65°=115°
- 相交线与平行线知识点:平行线的性质
- › 相交线与平行线知识点:平移
- › 相交线与平行线知识点:平行线的性质
- › 相交线与平行线知识点:平行线
- › 相交线与平行线知识点:相交线
- › 相交线与平行线学案
- 在百度中搜索相关文章:相交线与平行线知识点:平行线的性质
- 在谷歌中搜索相关文章:相交线与平行线知识点:平行线的性质
- 在soso中搜索相关文章:相交线与平行线知识点:平行线的性质
- 在搜狗中搜索相关文章:相交线与平行线知识点:平行线的性质
