。
解：（1）分析：由已知条件
，可以考虑使用均值不等式，但所求证的式子中有
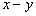，无法利用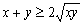
，故猜想先将所求证的式子进行变形，看能否出现
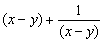型，再行论证．
证明：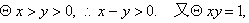
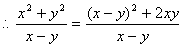
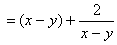
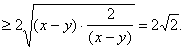等号成立
当且仅当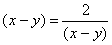
时．
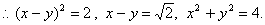
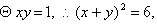
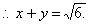由以上得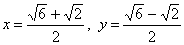
即当
时等号成立．
说明：本题是基本题型的变形题．在基本题型中，大量的是整式中直接使用的均值不等式，这容易形成思维定式．本题中是利用条件将所求证的式子化成分式后再使用均值不等式．要注意灵活运用均值不等式．
（2）∵ 
≥
，
≤
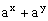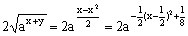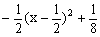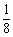，0
∴ 
≥
∴ 
≥
∴ 
≤
Tag:高考数学复习，高考数学复习大全，高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
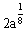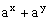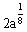
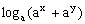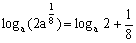
- 2017高考数学复习：不等式（一）
- › 2017马年春节对联：春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章：2017高考数学复习：不等式（一）
- 在谷歌中搜索相关文章：2017高考数学复习：不等式（一）
- 在soso中搜索相关文章：2017高考数学复习：不等式（一）
- 在搜狗中搜索相关文章：2017高考数学复习：不等式（一）