或
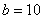 ,
,
若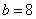 ,则
,则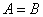 ,得
,得 ,即
,即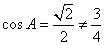 矛盾,故
矛盾,故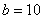 .
.
点评:在解三角形时,应注意多解的情况,往往要分类讨论.
例2.在三角形ABC中,已知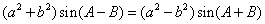 ,试判断该三角形的形状.
,试判断该三角形的形状.
解法一:(边化角)由已知得: ,
,
化简得 ,
,
由正弦定理得: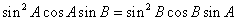 ,即
,即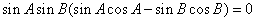 ,
,
又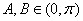 ,
,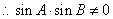 ,
,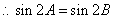 .
.
又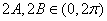 ,
,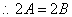 或
或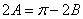 ,即该三角形为等腰三角形或直角三角形.
,即该三角形为等腰三角形或直角三角形.
解法二:(角化边)同解法一得: ,
,
由正余弦定理得: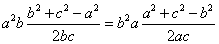 ,
,
整理得: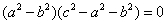 ,即
,即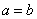 或
或 ,
,
即该三角形为等腰三角形或直角三角形.
点评:判断三角形形状主要利用正弦或余弦定理进行边角互化,从而利用角或边判定三角形形状.
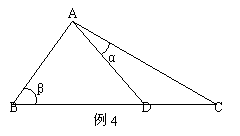
例3.如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=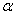
上一页 [1] [2] [3] [4] [5] [6] 下一页
- 2017高考数学复习:三角函数(四)
- › 2017马年春节对联:春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章:2017高考数学复习:三角函数(四)
- 在谷歌中搜索相关文章:2017高考数学复习:三角函数(四)
- 在soso中搜索相关文章:2017高考数学复习:三角函数(四)
- 在搜狗中搜索相关文章:2017高考数学复习:三角函数(四)
