裂项法是我们在速算与巧算中非常常用的一种,它是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的。
裂项法中有一些常用的公式:
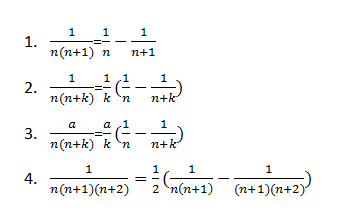
我们先来看一个非常简单的裂项法计算。
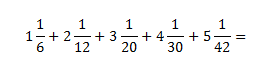
在上面这个算式中,我们可以简单将每一项拆分成带分数的整数部分和分数部分来分开计算。对分数部分的计算,我们可以利用公式1,进行简化。所以,
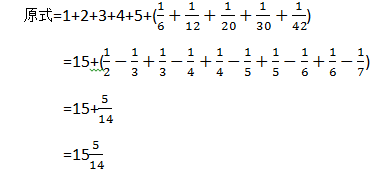
上述题目就是我们裂项法的一个简单的应用。这题中出现的分数让我们很快就能够看出如何裂项,是很明显的符合我们公式1的裂项要求的题目,下面我们再来看一题。
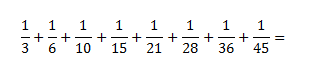
这一题中的分母并不如上一题中我们所熟悉的,不可以直接裂项。既然不能直接裂项,我们就需要在原题上做一定的变幻,再进行裂项。我们将原题先乘以将它变成能应用于公式1的裂项法然后再乘以2以抵消。所以,
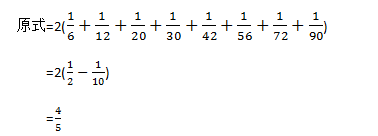
像这种类型的题目就是我们裂项法公式1的一个变形后的应用,遇见不能直接裂项的,我们可以将它先加以处理,转化成可以裂项的式子,这也说裂项法中常见的题目类型。
根据这个我们再看一下下面的这道例题:
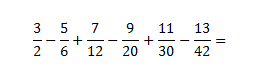
经观察,这题中的各项分母是符合我们一半裂项公式1的条件的,可以简单的看出,而对于分子来说,则是出现了一些变化,这些分子不是1了,我们再仔细观察,分子也是有一定规律的,不是相邻2项相减的裂项,而是相邻2项相加的裂项。所以,我们很容易可以将原式转化,
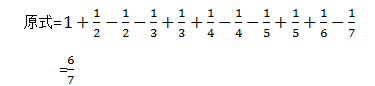
以上三题都是关于我们的裂项法最基础的公式1的应用和变形应用,类似的题型还有很多,多是万变不离其中。
对于公式1的应用我们就讲解到这里,公式2和3都是关于公式1的一个变形应用,下面我们来看看关于公式4的一些例题。首先先来一道很简单的例题。

在这题中,我们先是用了公式4来将3项相乘的分母拆分,然后再拆分出来的项中,我们很容易可以看出来,除了头尾2项,其他剩下的部分是可利用我们的公式1进行转化裂项的,故而这题其实是我们裂项法常用的两个公式的综合运用。
- 中考数学:分数裂项法知识点汇总
- › 怎样提高中考数学的解题能力
- › 2016中考数学复习攻略:三点帮你得高分
- › 2016哈市中考数学复习策略
- › 2016中考数学重要考点分析
- › 初三冲刺中考:2016中考数学复习计划
- › 2016中考数学复习计划总结(二)
- › 2016中考数学复习计划总结(一)
- › 中考数学抓牢基础重教材
- › 中考数学第三轮复习的形式和要求
- › 2016年中考数学复习指导
- › 2016中考数学复习:三角形及答案
- › 2016中考数学模拟试卷:因式分解
- 在百度中搜索相关文章:中考数学:分数裂项法知识点汇总
- 在谷歌中搜索相关文章:中考数学:分数裂项法知识点汇总
- 在soso中搜索相关文章:中考数学:分数裂项法知识点汇总
- 在搜狗中搜索相关文章:中考数学:分数裂项法知识点汇总
